Equitable access to COVID-19 vaccines makes a life-saving difference to all countries | Nature Human Behaviour

The SARS-CoV-2 virus is mutating over time, resulting in genetic variation over the course of the pandemic. On the basis of virology studies⁴⁸, we assume that SARS-CoV-2 mutates rapidly, but most of the mutations are neutral. Neutral mutations have little impact on the virus’s ability to cause infections. Some mutations at critical locations of the genetic sequence may change the virus’s transmissibility and severity. Here we extend the multiple-strain model^35,36,41 to characterize viral evolutionary dynamics. For country i, such dynamics are captured by the transmissibility matrix \({{{\mathcal{T}}}}\), the severity matrix \({{{{\mathcal{F}}}}}_{i}\) and the mutation matrix \({{{\mathcal{U}}}}\), all with dimensions M × M. M ≥ 2 represents the number of possible strains. The transmissibility matrix \({{{\mathcal{T}}}}\) and the severity matrix \({{{{\mathcal{F}}}}}_{i}\) are both diagonal matrices. \({{{{\mathcal{T}}}}}_{m}\) and \({{{{\mathcal{F}}}}}_{i,m}\) represent the transmissibility (the probability of disease transmission in a single contact multiplied by the average number of contacts per person per unit time; determined by the basic reproduction number and the infectious period) and the severity (the infection fatality rate) of strain m ∈ {1, 2, . . . , M}, respectively. We set a country-specific severity matrix to account for the heterogeneity in the health-care burden of COVID-19 and the age structure in different countries (Supplementary Note 3)^41,49,50. We assume a linear strain space and local movement by a one-direction stepwise mutation in the model⁴⁷. Each point in the strain space represents a single strain. More similar strains are closer in the strain space. The virus in strain m either remains as strain m with probability 1 − μ_m or mutates to strain m + 1 (one-direction stepwise mutation) with probability μ_m while adapting to a new host (please refer to Supplementary Note 4 for the details of the spreading process). Thus, we construct \({{{\mathcal{U}}}}\) as

The virus cannot evolve indefinitely, primarily because each nucleotide can only mutate to three others (for example, adenine can only mutate to thymine or guanine or cytosine), and the genome of SARS-CoV-2 has a limited number of nucleotides^51,52. As the virus evolves in the strain space, the probability of major new changes per infection decreases because fewer possible genome sequences remain. Thus, we assume that μ_m+1 = μ_m/λ. Since detected cases of reinfection are much rarer than postvaccination cases⁵³, we assume that (1) hosts recovered from either strain are immune to all other strains, and (2) hosts vaccinated for one strain exhibit a certain degree of cross-protection from other strains. The cross-immunity between the vaccine strain m and a mutant strain n is given by \({{\mathrm{e}}}^{-{(\frac{m-n}{d})}^{2}}\), the chance that the immunity induced by vaccines for strain m will provide immunity to strain n^47,54. Here, ∣m − n∣ represents the antigenic distance, and d is a fixed value representing the distance of antigenicity between the vaccine strain and a mutant strain when the cross-immunity is reduced to 1/e. This expression is based on the assumption that vaccine-induced immunity is less cross-reactive as the antigenic distance between the vaccine strain and a mutant strain increases. Suppose vaccines designed for strain m demonstrate an efficacy of η_mn and ϵ_mn against infection and death from strain n, respectively. Then, we define

Here we assume that all current cases are caused by strain 1, and only vaccines designed for strain 1 are provided. Thus, by taking m = 1, equation (2) can be simplified as

where η_n and ϵ_n represent vaccine efficacy against infection and death from strain n, respectively. We have already seen the emergence of more infectious and more harmful strains in the real world^17,18,19,20. For example, the hazard of death associated with the B.1.1.7 (Alpha) strain is estimated as 61% higher than with pre-existing variants, and the basic reproduction number of B.1.617.2 (Delta) is estimated at about 5–8, which is much higher than that of the original strain (2.79; ref. ⁵⁵). We thus incorporate these facts in our model by assuming that \({{{{\mathcal{T}}}}}_{1} < {{{{\mathcal{T}}}}}_{2} < … < {{{{\mathcal{T}}}}}_{M}\), since the stability of the virus increases (specifically, we assume that \({{{{\mathcal{T}}}}}_{n+1}=(1+\theta ){{{{\mathcal{T}}}}}_{n}\)); and that \({{{{\mathcal{F}}}}}_{i,n+1}\) is correlated with \({{{{\mathcal{T}}}}}_{n+1}(1-{\eta }_{n+1})\), which is proportional to the viral load. Thus, \({{{{\mathcal{F}}}}}_{i,1} < {{{{\mathcal{F}}}}}_{i,2} < … < {{{{\mathcal{F}}}}}_{i,M}\).

SVEIRD-based metapopulation model

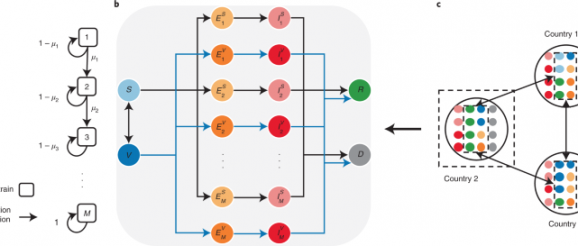
The proposed SVEIRD-based metapopulation model extends the classic susceptible–exposed–infectious–recovered model to account for the effects of viral mutations, vaccine updates, non-pharmaceutical interventions (NPIs) and restricted international mobility. Individuals in country i (with population size N_i) are divided into the following classes: susceptible individuals (S_i), vaccinated individuals (V_i), individuals exposed to strain m (not yet infectious) without vaccinal immunity (\({E}_{i,m}^{S}\)), individuals exposed to strain m (not yet infectious) with vaccinal immunity (\({E}_{i,m}^{V}\)), infectious individuals caused by strain m without vaccinal immunity (\({I}_{i,m}^{S}\)), infectious individuals caused by strain m with vaccinal immunity (\({I}_{i,m}^{V}\)), recovered individuals (R_i) and deceased individuals (D_i). Susceptible individuals are vaccinated at the vaccination rate ϕ_i(t) according to the global vaccine allocation strategy. We assume that vaccinated individuals gradually lose vaccinal immunity and become fully susceptible again at the rate ε. We demonstrate the contacts between susceptible individuals (vaccinated individuals) and infectious individuals as a diagonal matrix \({{{{\mathcal{C}}}}}_{i}^{S}(t)\) (\({{{{\mathcal{C}}}}}_{i}^{V}(t)\)) with dimensions M × M for country i at time t. The term \({{{{\mathcal{C}}}}}_{i}^{S}{(t)}_{m}\) represents the number of contacts between susceptible individuals and infectious individuals caused by strain m for country i at time t:

where c_i ∈ [0, 1] quantifies the effectiveness of NPIs for country i. Similarly:

Thus, the transition rate from S_i to \({E}_{i,m}^{S}\) is \({\sum }_{n}{[{{{{\mathcal{C}}}}}_{i}^{S}(t){{{\mathcal{T}}}}{{{\mathcal{U}}}}]}_{n,m}\). Similarly, the transition rate from V_i to \({E}_{i,m}^{V}\) is \({\sum }_{n}(1-{\eta }_{n}){[{{{{\mathcal{C}}}}}_{i}^{V}(t){{{\mathcal{T}}}}{{{\mathcal{U}}}}]}_{n,m}\). Exposed individuals become infectious with transition rate σ; thus, the incubation period is 1/σ.

To model how countries introduce and relax NPIs during the COVID-19 pandemic, we consider the reproduction-number-based adaptive policy adoption strategy^56,57,58, where more stringent NPIs are triggered when the local effective reproduction number exceeds a certain threshold, and NPIs are relaxed to less stringent when it falls below the threshold. Note that each country introduces or relaxes NPIs on the basis of the local effective reproduction number within each country, instead of the effective reproduction number for the metapopulation network^59,60,61. The details of the adaptive policy adoption strategy can be found in Supplementary Note 2.

Infectious individuals become either recovered or deceased at transition rate α; thus, the infectious period is 1/α. For individuals without vaccinal immunity, the transition rates from infectious (caused by strain m) to recovered and deceased are \((1-{{{{\mathcal{F}}}}}_{i,m})\alpha\) and \({{{{\mathcal{F}}}}}_{i,m}\alpha\), respectively; for individuals with vaccinal immunity, the transition rates from infectious (caused by strain m) to recovered and deceased are \([1-(1-{\epsilon }_{m}){{{{\mathcal{F}}}}}_{i,m}]\alpha\) and \((1-{\epsilon }_{m}){{{{\mathcal{F}}}}}_{i,m}\alpha\), respectively. Individuals recovered from either strain are assumed to be immune to all other strains. We assume that infectious and deceased individuals do not travel across countries. G_ij(t) denotes the number of individuals travelling from country i to country j at time t. For simplicity, we assume a dynamic and undirected international mobility network in this model and thus define G_ij(t) as

Here, γ is the average mobility rate, \({A}_{i}(t)={N}_{i}-{D}_{i}(t)-{\sum }_{m}[{I}_{i,m}^{S}(t)+{I}_{i,m}^{V}(t)]\) is the number of individuals allowed to travel from country i to other countries at time t, and P_ij is the fraction of individuals travelling from country i to country j and is assumed to be constant. ∑_jP_ij = 1, and P_ii = 0. We denote F_ij as the number of passengers travelling from country i to country j per day, and F_i = ∑_jF_ij. Then, P_ij = F_ij/F_i. We obtain F_ij by averaging the aggregated number of seats on scheduled commercial flights between countries per day in the year 2020 (Supplementary Note 6). All possible state transitions within each country are shown in Fig. 1. The disease transmission dynamics is described by the following equations:

Global vaccine allocation model

We denote the cumulative global vaccine supply at time t as φ(t). On the basis of the predicted exponential growth in the global vaccine supply in the coming months³⁷, we assume that φ(t) first increases exponentially until the maximum daily production capacity is reached at time τ and then grows gradually at the maximum daily production capacity φ(τ) − φ(τ − 1) until the end of the epidemic:

The parameter v quantifies how fast the manufacturers worldwide are ramping up the production of vaccines. The global supply of vaccines at time t is φ(t + 1) − φ(t). The number of vaccines allocated to each country depends on the global supply of vaccines, the global vaccine allocation strategy and the demand for vaccines for each country. Here we model two sets of global vaccine allocation strategies: equitable and inequitable ones. Under equitable vaccine allocation strategies, available vaccines at each time will be allocated to each country on the basis of the prioritization criteria. In inequitable vaccine allocation strategies, a minimum fraction χ of vaccines available at each time are purchased by HICs, and the remaining vaccines are allocated to LMICs. Then, in both the HIC and LMIC groups, vaccines are allocated to each country on the basis of the prioritization criteria. Countries are classified into HICs or LMICs according to their incomes and their capability for mass production of COVID-19 vaccines. The basic income classification is based on the gross national income per capita (calculated using the World Bank Atlas method in US dollars). We summarize the basic income classification results in Table 1. Specifically, HICs in our model include high-income countries in Table 1 plus China and Russia, because of their capability for mass production of COVID-19 vaccines. The remaining countries are defined as LMICs. We consider four prioritization criteria in both equitable and inequitable vaccine allocation strategies:

Population size: Priority to countries with larger population sizes.

Prevalence: Priority to countries with a higher number of active cases (currently infectious cases) per capita.

Mortality rate: Priority to countries with a higher number of new deaths during the past two weeks as a share of the total population.

Incidence: Priority to countries with a higher number of new cases during the past two weeks as a share of the total population.

All prioritization criteria are being updated dynamically on the basis of the epidemic evolution within each country (Supplementary Note 5). Currently, some vaccines require two doses to provide broader and longer-lasting immunity against the virus, such as Pfizer-BioNTech and Moderna⁶², while some vaccines need only one dose, such as Johnson & Johnson’s vaccines. For simplicity, we assume that (1) all vaccines are administered with a two-dose schedule, (2) two doses are administered simultaneously, (3) the body can build full vaccinal immunity immediately after vaccination and (4) the upper bounds of daily vaccination rates for HICs and LMICs are the maximum daily vaccination rates achieved by HICs and LMICs from 1 December 2020 to 15 June 2021 (t = 0).

Calculation of the average lives saved by vaccine donations

We denote \({\overline{D}}_{i,{\mathrm{ineq}}}\) and \({\overline{D}}_{i,{\mathrm{don}}}\) as the cumulative mortality for country i at the end of the simulation under inequitable and allow-donation vaccine allocation strategies, respectively. The average lives saved by vaccine donations (the difference between the cumulative mortality under the allow-donation allocation strategy and that under the inequitable allocation strategy) as the share of the national population in HICs and LMICs are denoted by r_H and r_L, respectively:

Here, H and L denote the set of HICs and LMICs, respectively; and ∣H∣ and ∣L∣ denote the number of HICs and LMICs, respectively.

In all simulations, t = 0 corresponds to 15 June 2021. We roughly take \({E}_{i,m}^{S}(0)=0\), \({E}_{i,m}^{V}(0)=0\), \({I}_{i,m}^{V}(0)=0\) and \({I}_{i,m}^{S}(0)=0\) (m ≠ 1). V_i(0) is estimated by the number of individuals that are fully vaccinated at t = 0. \({I}_{i,1}^{S}(0)\) is estimated by the number of currently active cases at t = 0. R_i(0) and D_i(0) are estimated by the cumulative numbers of recovered and decreased individuals at t = 0. Thus:

Due to severe under-reporting worldwide, especially in LMICs with low testing rates, we adopt the probabilistic bias analysis^63,64 to correct the numbers of infections, recoveries, deaths and active cases for all countries. Please refer to Supplementary Note 1 for a detailed description of the data correction.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.