Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19 | Nature Human Behaviour
a–i, Evolution of the number of new cases (a,d,g), the outbreak size (b,e,h) and the effective reproductive number (c,f,i) as a function of time in each situation studied. Results for the SARS-CoV-2 transmission dynamics are shown for the unmitigated scenario (a–c) and the two social-distancing interventions considered: LIFT (d–f) and LET (g,h) scenarios. In both LIFT and LET scenarios, we considered the closure of schools and non-essential places for eight weeks. This is the strictest lockdown period, which is followed by a partial lifting of the stay-at-home policy, the duration of which is set to four weeks. During the partial lifting, all places in the community layer are open except mass-gathering locations (such as restaurants, theatres, and others; see Supplementary Information). Finally, a full reopening takes place after the period of partial lifting ends (relevant events are marked with vertical lines). In d–f, no other measures are adopted concurrently to the lifting of the restrictions, whereas in g–i, the reopening is accompanied by an active policy consisting of testing the symptomatic individuals, home isolating them and quarantining (Q.) their household and the households of a fraction of their contacts, as indicated. Note that the vertical scales of graphs in a,d,g are not the same and that both the number of new cases and total cases are per 1,000 inhabitants. x-axes show dates in 2020. Feb, February; Mar, March; Apr, April; Jun, June; Jul, July; Aug, August; Sep, September; Oct, October; Nov, November; Dec, December. In all panels, the solid line represents the average over 10,000 simulations and the shaded region represents the 95% CI.
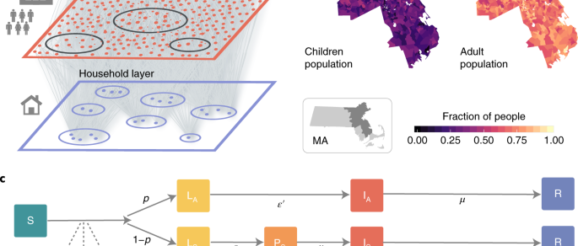
Our synthetic population constitutes around 85,000 nodes, of which 64,000 are adults and 21,000 are children (defined as individuals aged 17 or less), as shown in Fig. 1b. The total number of interactions among these individuals before social distancing is given by more than five million edges, see Supplementary Information for a more detailed description.
Community-weighted contact network
The community network is approximated using six months of data observation in the Boston area from anonymized users who have opted-in to provide access to their location data anonymously through a GDPR-compliant framework provided by Cuebiq. Individuals performing the analysis were legally required to never single out identifiable individuals and not make attempts to link these data to third-party data about an individual. In this layer, each agent in our synthetic population represents an anonymous individual of the real population. The data allow us to understand how infection can propagate in each layer by estimating colocation of two individuals in the same setting. We use a large database of 83,000 places from Foursquare application programming interface in the BMA. Specifically, the weight, \({\omega }_{{C}_{ij}}\), of a link between individuals i and j within the workplace plus community layer is computed according to the expression:
where Tip is the total time that individual i was observed at place p and Ti is the total time that individual i has been observed at any place set within the workplace plus community layer. Note that while the mobility dataset we use is large, colocation events between individuals are still quite sparse. Because of this sparsity, and to protect individual privacy in our analysis, we have adopted this probabilistic approach to measure co-presence in all locations mapped in the dataset. Since agents are representative of the different census areas and groups of the Boston area, our probabilistic approach is a good proxy for the real probability of co-presence between those groups and areas when networks are scaled up to the total population of the Boston area, which is approximately 4,628,910 inhabitants. Finally, for robustness and computational reasons, we have included only links for which \({\omega }_{{C}_{ij}}>0.01\).
Household-weighted contact network
We first localize individuals’ approximate home place according to the US census block group. Then we assign a type of household based on Table B11016: Household Type by Household Size from US Census 2018 (ref. 9), and mix individuals that live in the same block according to statistics of household type and size. Finally, children are assigned to households (see the Supplementary Information for a more detailed description). We also assign individuals to an age group, on the basis of Table B01001: Sex and age from the US Census 2018. To assign weights, we assume that the probability of interaction within a household is proportional to the number of people living in the same household (well-mixing). Therefore, the weight, \({\omega }_{{H}_{ij}}\), of a link between individuals i and j within the same household is given by:
where nh is the number of household members. This fraction is assumed to be the same for all individuals in the population.
School-weighted contact network
To calculate the weights of the links at the school layer, we mix together all children that live in the same school catchment area. Interactions are considered well-mixed; hence, the probability of interaction at a school is proportional to the number of children at the same school. Therefore, the weight, \({\omega }_{{S}_{ij}}\), of a link between children i and j within the same school is given by:
where ns is the number of school members.
Calibration of intra-layer links
Within each connected component of the network in each layer (for example, a household or a school), the links between nodes are weighted to account for the effective daily number of contacts. For example, if we consider a school, while a student can potentially contact all her or his schoolmates, she or he only meet a relatively small fraction of them on a daily basis, as estimated in empirical studies on mixing patterns24,25. To account for this, we calibrate the weight of the links in each layer of the synthetic network26 so that the mean number of daily contacts matches the estimation provided in Mistry et al.27 (details in Supplementary Information). On the basis of the analysis of contact survey data from 9 countries24,25,28,29, this study estimated the mean number of daily contacts at 10.86, 4.11 and 11.41 in the community and workplace, household and school layers, respectively.
Stochastic simulations of COVID-19 dynamics
We describe the SARS-CoV-2 transmission process using a discrete-time susceptible–latent–infected–removed (SLIR) stochastic model, with some additional compartments to incorporate the special characteristics of SARS-CoV-2 infection (Fig. 1c). In particular, at each time-step t (1 d), the infectious asymptomatic (IA), infectious symptomatic (IS) and pre-symptomatic (PS) individuals can transmit the disease to susceptible (S) individuals with probability rβ, β and βS, respectively. If the transmission is successful, the susceptible node will move to the latent asymptomatic state (LA) with probability p or to the latent symptomatic state (LS) with probability (1 − p). A latent asymptomatic individual becomes infectious asymptomatic after a period (ϵʹ)−1, whereas latent symptomatic individuals transition, after a period ϵ−1, to the pre-symptomatic (PS) compartment. The average period to develop the disease and move to the infectious symptomatic state is γ−1. Infectious asymptomatic nodes are removed (R) after an average of μ steps. Conversely, infectious symptomatic nodes can either recover after that period with probability (1 − α) or, with probability α, these nodes will need hospitalization. It is considered that due to their symptoms they will self-isolate at home after an average period of μ−1. Then, depending on the severity of the symptoms, after a period δ−1 the individual will end in hospitalization with probability (1 − χ) or require hospitalization and ICU care with probability χ. Finally, individuals that are either hospitalized or in ICU become removed with probability μH or μICU, respectively. We initialize the model in the city of Boston by selecting an attack rate on 17 March 2020 of 1.5% (a sensitivity analysis of this quantity is provided in the Supplementary Information).
Social-distancing strategies
To simulate social-distancing measures, we modify the synthetic population such that:
School closures are simulated by removing all the schools from the system simultaneously.
Partial ‘stay-at-home’ assumes that all places are open except restaurants, nightlife and cultural places. Closures of these places are simulated by removing the interactions that occur in any place that falls into that category according to Foursquare’s taxonomy of places. This is the situation after the first reopening.
Full lockdown and confinement assume that schools and all non-essential workplaces are closed. Here we close all workplaces except essential ones and remove interactions that occur there. Essential workplaces are: hospitals, salons, barbershops, grocery stores, dispensaries, supermarkets, pet stores, pharmacies, urgent care centres, dry cleaners, drugstores, maternity clinics, medical supplies and petrol stations.
The connectivity distributions for each of the scenarios simulated as well as other statistics related to the effects of the lockdown are shown in the Supplementary Information.
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
