Social network-based distancing strategies to flatten the COVID-19 curve in a post-lockdown world | Nature Human Behaviour

Generation of stylized networks

The stylized binary network x that represents interaction opportunities is based on the typical contact people had in a pre-COVID-19 world. It is generated stochastically as the composite of four sub-processes that follow fairly standard ideal-type network-generating approaches. Representing place of residence, actors are assumed to have a fixed geographic location, as determined by coordinates in a two-dimensional space. They are members of groups (such as households) and institutions (such as schools or workplaces) and have individual attributes (such as age, education or income). Network ties are generated so that actors have some connections to geographically close alters, some ties to members of the same groups (representing, for example, co-workers), some ties to alters with similar attributes (for example, similar age) and some ties to random alters in the population. Jointly, these sub-processes create networks that have realistic values of local clustering, path lengths and homophily. All ties in the network are defined as undirected. The number of actors in the network is denoted by n. For the benchmark scenario presented in Fig. 4, n = 2,000, and for the variations and robustness analyses, n = 1,000, unless otherwise stated. In particular, the network sub-processes are defined as follows.

The first sub-process represents tie formation based on geographic proximity³⁸. First, all actors in the network are randomly placed into a two-dimensional square. Second, each actor draws the number of contacts it forms in this sub-process d_geo,i from a uniform distribution between d_geo,min and d_geo,max; for example, if d_geo,min = 10 and d_geo,max = 20, every actor forms a random number of ties between 10 and 20 in this sub-process. Third, the user-defined density in geographic tie-formation d_geo defines the geographic proximity of contacts drawn, so that actor i randomly forms d_geo,i ties among those d_geo,i/d_geo that are close in Euclidean distance from actor i. For example, if actor i is posed to form d_geo,i = 12 ties and d_geo = 0.5, the actor randomly choses 12 out of the 24 closest alters to form a tie to. Across all simulated networks, we set d_geo = 0.3. Fourth, unilateral choices (where only i selected j but not vice versa) are symmetrized so that a non-directed connection exists between the actors.

The second sub-process represents tie formation in organizational foci (for example, workplaces)³⁹. First, each actor is randomly assigned to a group so that all groups have on average m members. Second, each actor forms ties at random to other members within the same groups with a probability of g_groups. For example, when m = 10 and g_groups = 0.5, a tie from each actor to every alter in the same group is formed with a probability of 50%. Third, unilateral ties are symmetrized as above.

The third sub-process represents tie formation based on homophily (that is, seeking similarity); for example, similarity in age or income²¹. First, each actor is assigned an individual attribute a_i between 0 and 100 with uniform probability (the scale of a_i cancels later in the model). Second, for each actor, the normalized similarity sim_i,j to all alters j is calculated, which is 1 minus the absolute difference between a_i and a_j for actor j, divided by 100 (the range of the variable), so that sim_i,j = 1 when i and j have the identical value of a, and sim_i,j = 0 if they are at opposite ends of the scale. Third, each actor draws the number of contacts it forms in this sub-process d_homo,i from a uniform distribution between d_homo,min and d_homo,max. Fourth, each actor creates d_homo,i ties to alters j in the networks with a probability that is proportional to (sim_ij)^w, where higher values of w mean that individuals prefer more similar others. Across all reported simulations, we set w = 2. Fifth, unilateral ties are symmetrized as above.

The fourth sub-process represents haphazard ties that are not captured by any of the above processes. Here, simply, z ties per actor are created with respect to randomly chosen alters.

Definition of simulation model

Let the binary network x represent interaction opportunities between n individuals, labelled from 1 to n. Each node i can be characterized by a set of attributes \(\left( {a_i^k} \right)\) (for example, age or location).

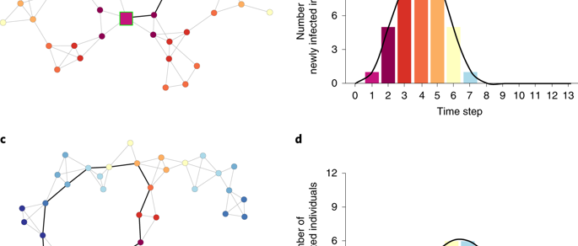
Our model aims to reproduce the process of individuals interacting with some of these potential contacts. Similar to the classic SIR model²⁶ (in which individuals are susceptible, infectious or recovered) and its SEIR extension²⁷ (in which they are susceptible, exposed, infectious and then recovered), we assume that individuals can be in four different states: either susceptible to the disease, exposed (infected but not yet infectious), infectious or recovered. Infection occurs through social interactions, which are modelled in a similar fashion to the dynamic actor-oriented model³⁴ developed for relational events. More specifically, our model comprises the following steps:

At each step of the process, one individual is picked at random and initiates an interaction with the probability π_contact.

An actor initiating an interaction can only pick one interaction partner. Only potential partners as defined by the network x can be chosen. The decision to interact is unilateral and depends on characteristics of the two persons through a probability model p.

An infectious individual infects a healthy person when they interact, who then becomes exposed. This contagion occurs with the probability π_infection.

After a fixed number of steps T_exposure, an exposed individual becomes infectious.

After becoming infectious, recovery occurs within T_recovery steps. Once recovered, individuals can no longer be infected.

The process ends once there is no longer anyone exposed or infectious.

The steps of the model are illustrated in Fig. 3. Note that the mechanics of the infection align with previously proposed agent-based versions of the SIR and SEIR models^40,41. Together, the probabilities π_contact and π_infection play a similar role to the classic infectivity rate β in SIR and SEIR models. The rate β models the average number of contacts per person (modelled here through π_contact) and the likelihood of infection (represented by π_infection); however, the equivalence is not direct due to the added step of the interaction probability p. The exposure and recovery times replace the classic exposure and recovery rates (often traditionally denoted as σ and γ) in a straightforward manner.

We turn to the definition of the probability model p. Let N_i be the set of potential contacts, or alters j of a given individual i in the network x. We define for each step t of the process: L_i(j,t) as the number of previous interactions between i and an alter j, within the past λ interactions of i. In our simulations, the number λ was arbitrarily set to 2 but can be adjusted easily in the replication files.

For each alter \(j \in N_i\), the value s(i,j) represents the statistic driving the strategical choice of i to pick j. Specifically, we define three different ways depending on whether the homophily, triadic (that is, strengthening community) or repetition bubble strategy is chosen (however, other arbitrary statistics can be defined). The statistic s_similarity accounts for the level of similarity between i and j given a set of attributes; s_community corresponds to the number of alters they share, and s_repetition is the count of previous interactions within the past λ contacts of i. In practice, these statistics are calculated as:

The probability for i to pick j is defined as a multinomial choice probability⁴², follo wing the logic of previous relational event³⁴ and stochastic network models³². The intuition behind this distribution is that each potential partner in N_i is assigned an objective function value, and choosing a partner is based on these values. Mathematically, the objective function is an exponentiated linear function of the statistic s(i,j), weighted by a parameter α. We further assume that individuals can reduce a certain percentage of their interactions. Considering the probability π_contact of initiating an interaction in the first place, the relevant probability distribution becomes:

These probabilities can be loosely interpreted in terms of log-transformed odds ratios, similar to logit models. Given two potential partners j₁ and j₂ for whom the statistic s increases by one unit (that is, s(i,j₂) = s(i,j₁) + 1), the following log ratio simplifies to:

For example, if we use s = s_repetition and α_repetition = log[2], the probability of picking one alter present in the past contacts of i is twice as high as picking another alter who is not.

Calibration of model parameters

The strategy of picking an interaction partner at random corresponds to the model without any statistic s, reducing the probability distribution to a uniform 1. For the three other strategies, the parameters α_similarity, α_community and α_repetition are adjusted to keep the models comparable.

To this end, we use the measure of explained variation for dynamic network models devised by Snijders³⁵. This measure builds on the Shannon entropy and can be applied to our model to assess the degree of certainty in individual’s choices. For a given individual i at a step t, this measure is defined as:

Intuitively, this measure equals 0 in the case of the random strategy where the probability of picking any alter is identical. It increases whenever some outcomes are favoured over others and equals 1 if one outcome has all of the probability mass.

Since the model assumes that all individuals are equally likely to initiate interactions, we can average this measure over all actors. Moreover, in the case of the repetition strategy, the measure is time dependent. Thus, we use its expected value over the whole process. We finally use the following aggregated measure to evaluate the certainty of outcomes of a specific strategy:

For this article, we first fix the parameter α_repetition at a value of 2.5 and calculate an estimated value \(\widehat {R_{\rm{H}}}\left( {\pi _{{\rm{contact}}},\alpha _{{\rm{repetition}}}} \right)\) of this measure. This experience-based parameter choice results in an associated R_H value between 0.3 and 0.5 in the different scenario, which is realistic in terms of size (see the definition above). To compare this model with others, we then define the parameters α_similarity and α_community that verify:

using a standard optimization algorithm. The average parameters across simulations for the different network scenarios are α_community = 0.75 and α_similarity = 17.6. While the latter parameter appears large, note that the associated statistic s_similarity ranges from 0 to 1, with most realized values close to 1. The R code associated with all of the calculations is provided in the online repository referenced in the Code Availability statement.

Parametrization of the different simulations

Unless otherwise specified, all simulations use π_contact = 0.5 except for the null model, which uses π_contact = 1. In all simulations except those that vary the infectiousness, π_infection = 0.8. Unless otherwise noted, T_exposure = 1n and π_infection = 4n. Given the substantial computational burden involved in conducting the simulations, 48 repetitions were run for networks with n ≤ 1,000, with 40 for larger networks. Experiments varying T_exposure and π_infection used 24 repetitions.

For the experiments that vary the structure of the underlying network and the network size, the parameters that guide the stochastic network creation are presented in Supplementary Table 1. Descriptive statistics of these networks are presented in Supplementary Table 2. The underlying networks that are used in the other variation experiments are generated according to the parameters denoted ‘1: baseline’ in Supplementary Table 1.

The four experiments that vary the time during which individuals are in the exposed state before becoming infectious use values for T_exposure of 0, 1n, 2n, 3n and 4n.

The four experiments that vary the infectiousness of the disease use values for π_infection of 0.55, 0.65, 0.80 and 0.95.

The experiment that used geography as the basis of the homophily strategy was created according to the ‘1: baseline’ parameters but used the Euclidean distance in geographic placement as the basis for choosing interaction partners in the homophily strategy. The two experiments on multidimensional homophily used underlying networks created following the ‘1: baseline’ parameters, with the exception that instead of one homophilous attribute, two attributes were defined and the number of ties created according to the homophily parameter was split evenly between the two dimensions. The homophily strategy used for the simulated infection curves in the two scenarios differs in the sense that in the first, individuals interact according to minimizing the absolute difference in both attributes. In the second scenario, only the first attribute is used as the basis of the homophily strategy and the second attribute is ignored.

For the experiments using mixed strategies, the probability of partner choice \(p\left( {i \to j} \right)\) can depend on a vector of statistics and parameters³⁴. The entropy based on a set parameter vector was used to calibrate the parameter for the homophily and triadic closure strategy as comparison cases. Parameter choices rely on experimentation to result in similar entropy values to when using single strategies. For the mixed strategy of repetition and homophily, the parameters were set to α_similiarity = 7 and α_repetition = 1.6. For the mixed strategy of repetition and triadic closure, the parameters were set to α_community = 0.35 and α_repetition = 1.6. For the mixed strategy of homophily and triadic closure, the parameters were set to α_similiarity = 6 and α_community = 0.35. For the mixed strategy incorporating all three, the parameters were set to α_similiarity = 4, α_community = 0.3 and α_repetition = 1.2.

The simulated average infection curves for all experiments can be found in Extended Data Figs. 1–7. Descriptive results for the simulations, in terms of delay of peak, height of peak and total number infected at the end of the simulation, are presented in Supplementary Table 3. Note that the descriptive statistics in this table present the averages of characteristics of the repetitions of the simulated infection curves, which are not the same as the characteristics of the average infection curves as presented in Extended Data Figs. 1–7.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.