State-level needs for social distancing and contact tracing to contain COVID-19 in the United States | Nature Human Behaviour

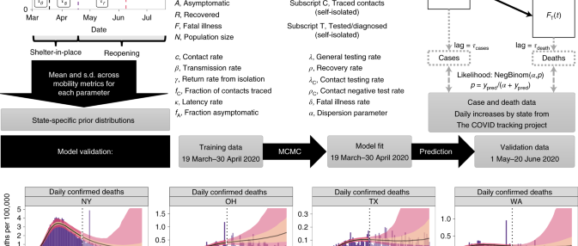
Our overall approach is as follows: (1) develop a mathematical model (an SEIR-type compartmental model)^18,19 that incorporates social-distancing data, case identification via testing, isolation of detected cases and contact tracing; (2) assess the model’s predictive performance by training (calibrating) it to reported cases and mortality data from 19 March to 30 April 2020 and validating its predictions against data from 1 May to 20 June 2020; and (3) use the model, trained on data to 22 July 2020, to predict future incidence and mortality. The final stage of our approach predicts future events under a set of scenarios that include increased case detection through expansion of testing rate, contact tracing and relaxation or increase of measures to promote social distancing. All model fitting is performed in a Bayesian framework to incorporate available prior information and address multivariate uncertainty in model parameters.

Model formulation

We modified the standard SEIR model to address testing and contact tracing, as well as asymptomatic individuals. A fraction f_A of those exposed (E) to enter the asymptomatic A class (divided into A_U for untested and A_C for contact traced) instead of the infected I class, which in our model formulation also includes infectious presymptomatic individuals. With respect to testing, separate compartments were added for untested, ‘freely roaming’ infected individuals (I_U), tested/isolated cases (I_T) and fatalities (F_T). Following recovery, untested infected individuals (I_U) and all asymptomatic individuals move to the untested recovered compartment, I_U, and tested infected individuals move to the tested recovered compartment, I_T. In balancing considerations of model fidelity and parameter identifiability, we made the reasonably conservative assumptions that all tested cases are effectively isolated (through self-quarantine or hospitalization) and thus unavailable for transmission, and that all COVID-related deaths are identified/tested.

With respect to contact tracing, the additional compartment S_C represents unexposed contacts who undergo a period of isolation during which they are not susceptible before returning to S, while E_C, A_C and I_C represent contacts who were exposed. Again, the reasonably conservative assumption was made that all exposed contacts undergo testing, with an accelerated testing rate compared to the general population. We assume a closed population of constant size, N, for each state.

The ordinary differential equations governing our model are as follows:

where c is the contact rate between individuals, β is the transmission probability per infected contact, f_C is the fraction of contacts identified through contact tracing, 1/γ is the duration of self-isolation after contact tracing, 1/κ is the latent period, f_A is the fraction of exposed who are asymptomatic, λ is the testing rate, δ is the fatality rate, ρ is the recovery rate and λ_C and ρ_C are the testing and recovery rates, respectively, of contact-traced individuals. The testing rates λ and λ_C, the fatality rate δ and the recovery rate of traced contacts ρ_C are each composites of several underlying parameters. The testing rate defined as

where F_test,0 is the current testing coverage (fraction of infected individuals tested), Sens_test is the test sensitivity (true positive rate) and k_test is the rate of testing for those tested, with a typical time-to-test equal to 1/k_test. The time-dependence term models the ramping up of testing using a logistic function with a growth rate of 1/τ_T d⁻¹, where T50_T is the time where 50% of the current testing rate is achieved. Similarly, for testing of traced contacts, the same definition is used with the assumption that all identified contacts are tested, F_test,0 = 1 and at a faster assumed testing rate, k_C,test:

Because all contacts are assumed to be tested, the rate ρ_C at which they enter the ‘recovered’ compartment, R_U is simply the rate of false negative test results:

The fatality rate is adjusted to maintain consistency with the assumption that all COVID-19 deaths are identified, assuming constant IFR. Specifically, we first calculated the fraction of infected that is tested and positive:

Then the case fatality rate CFR(t) = IFR/f_pos(t). Because CFR = δ/(δ + ρ), this implies

The model is ‘seeded’ N_initial cases on 29 February 2020. Because in the early stages of the outbreak there may be multiple ‘imported’ cases, we fit to data only from 19 March 2020 onwards, 1 week after the US travel ban was put in place³¹.

Our model is fit to daily case y_c and death y_d data (cumulative data are not used for fitting because of autocorrelation). To adequately fit the case and mortality data, we accounted for two lag times. First, a lag is assumed between leaving the I_U compartment and public reporting of a positive test result, accounting for the time it takes to seek a test, obtain testing and have the result reported. No lag is assumed for tests from contact tracing. Second, a lag time is assumed between entering the fatally ill compartment F_T and publicly reported deaths. Additionally, we use a negative binomial likelihood to account for the substantial day-to-day over-dispersion in reporting results. The corresponding equations are as follows:

In this parameterization, because the dispersion parameter α → ∞, the likelihood becomes a Poisson distribution with expected value y_pred,[c,d], whereas for small values of α there is substantial interindividual variability. Case and death data were sourced from The COVID Tracking Project³².

Finally, we derived the time-dependent reproduction number, R(t) and the effective reproduction number, R_eff(t) of this model, given by

R_eff(t) is the average number of secondary infection cases generated by a single infectious individual during their infectious period in partially susceptible population at time t. It is equal to the product of the transmission risk per contact of an infectious individual with their untraced contacts, c × β × (1 − f_C), times their average duration of infection, \(\left( {\frac{{1 – f_{\mathrm{A}}}}{{\lambda + \rho }} + \frac{{f_{\mathrm{A}}}}{\rho }} \right)\), and the portion of contacts that are susceptible, \(\frac{{{{S}}(t)}}{N}\). This accounts for the relative contribution of asymptomatic, \(c \times \beta \times \left( {1 – f_{\mathrm{C}}} \right)\left( {\frac{{f_{\mathrm{A}}}}{\rho }} \right) \times \frac{{{{S}}(t)}}{N}\) and symptomatic infection, \(c \times \beta \times (1 – f_{\mathrm{C}})\left( {\frac{{1 – f_{\mathrm{A}}}}{{\lambda + \rho }}} \right) \times \frac{{{{S}}(t)}}{N}\). Using posterior samples for all 50 states and the District of Columbia, we conducted an analysis of variance using a linear model to characterize the contributions to the combined interstate and intrastate variation in R_eff. Specifically, we used a linear model for R_eff with the model parameters R₀, η, θ_min, r_max, f_C, f_A, λ and ρ as predictors, and evaluated the percentage of variance in R_eff contributed by each parameter.

Incorporating social distancing, enhanced hygiene practices and reopening

The impact of social distancing, hygiene practices and reopening was modelled through a time dependence in the contact rate, c and the transmission probability per infected contact, β:

The θ(t) function parameterized social distancing during the progression to shelter-in-place, and is modelled as a Weibull function:

which starts as unity and decreases to θ_min, with τ_θ being the Weibull scale parameter and n_θ the Weibull shape parameter (Fig. 1).

The r(t) function parameterized relative increase in contacts due to reopening after shelter-in-place, with r = 1 corresponding to a return to baseline c = c_0.

The term r(t) is 0 before t_r, linear between t_r and t_rmax and constant at a value of r_max after that, and made continuous by approximating the Heaviside function by a logistic function. The reopening time is defined as τ_s days after τ_θ, and the maximum relative increase in contacts r_max happens τ_r days after that.

We selected the functional form above for c(t) because it was found to be able to represent a wide variety of social-distancing data, including mobile phone mobility data from Unacast³³ and Google³⁴ as well as restaurant booking data from OpenTable³⁵. We used these different mobility sources to derive state-specific prior distributions because different social-distancing datasets had different values for θ_min, τ_θ, n_θ, τ_s, r_max and τ_r (Supplementary Fig. 1).

With respect to the reduction in transmission probability β, we assumed that during the shelter-in-place phase, hygiene-based mitigation paralleled this decline with an effectiveness power η, and that this mitigation continued through reopening.

Finally, we define an overall reopening parameter Δ that measures the rebound in disease transmission, c × β relative to its minimum, defined to be 0 during shelter-in-place (that is, R(t) is at a minimum) and 1 when all restrictions are removed (when R(t) = R₀), which can be derived as:

Our model is illustrated in Fig. 1, with parameters and prior distributions listed in Table 1.

Scenario evaluation

We used the model to make several inferences about the current and future course of the pandemic in each state. First, we consider the effective reproduction number. Two time points of particular interest are the time of minimum R_eff, reflecting the degree to which shelter-in-place and other interventions were effective in reducing transmission, and the final time of the simulation, 22 July 2020, reflecting the extent to which reopening has increased R_eff. Additional parameters of interest are the current levels of reopening Δ(t), testing λ and contact tracing f_C.

We then conducted scenario-based prospective predictions using our model’s parameters as estimated to 22 July 2020. We then asked the following questions:

Assuming current levels of reopening, what increases in general testing λ and/or contact tracing f_C would be necessary to bring R_eff < 1?

What level of reopening Δ can maintain R_eff < 1 under four different scenarios: current values of testing and contact tracing, doubling testing, double tracing and doubling both testing and tracing?

What will be the rates of new cases and deaths under different scenarios? Specifically, we evaluate the impact of increases in testing and contact tracing under current levels of reopening, as well as increases or decreases of 25 or 50%.

For (1), we evaluated the posterior probability that R_eff < 1 under scaling transformations λ → λ × μ_λ and f_C → f_C × μ_C with scaling factors μ_λ and μ_C:

We additionally derived ‘critical’ values of μ_C and μ_λ where R_eff(t) < 1 under the conditions of increased testing alone (μ_C = 1), increased contact tracing alone (μ_λ = 1) and equal increases in testing and tracing (μ_C = μ_λ). We also performed the same analysis under a full reopening scenario (that is, setting S(t) = 1, c = c₀ and β = β₀).

For (2), we rearranged the equation for R_eff in terms of the reopening parameter Δ:

We then fixed the scaling factors at 1 or 2, and solved the above equation to determine the percentage of reopening (Δ_crit) that can be achieved while keeping R_eff < 1. Values of Δ_crit ≥ Δ(t) indicate the additional degree of reopening possible while maintaining R_eff < 1, while values of Δ_crit < Δ(t) indicate that reduction of reopening is needed. To convert back to testing and contact-tracing rates, we multiplied the scaling factors μ_C and μ_λ by the original values of f_C and λ, respectively.

Finally, for (3), we additionally evaluated changes in reopening Δ → Δ + Δ_Δ for Δ_Δ values of +25% (+50%) or −25% (−50%), for a total of 20 scenarios (four different levels of testing and tracing and five different levels of reopening). We then ran the SEIR model forward in time to 30 September 2020. For all three intervention parameters, μ_C, μ_λ and Δ_Δ, we assumed a ramp-up period of 2 weeks from 1 to 14 August 2020.

To summarize the relative need for mitigation in each state, we categorized states based on which scenarios resulted in the IQR of R(t) < 1 on 15 August 2020. The categories were defined as follows:

Very Low: can reopen further by >25% while maintaining R(t) < 1

Low: can reopen further by <25% with up to 2× increase in testing while maintaining R(t) < 1

Moderate: requires 2× contact tracing or reversal of reopening by 25% to bring and maintain R(t) < 1

High: requires multiple interventions (2× testing, 2× contract tracing and reversal of reopening by 25%) to bring and maintain R(t) < 1

Very High: combining 2× testing, 2× contact tracing and reversal of reopening by 50% is needed to bring and maintain R(t) < 1

We use R(t) instead of R_eff(t), to minimize the impact of heterogeneity and uncertainty in the value of S(t)/N on our results. Thus, requiring R(t) < 1 provides greater assurance of state-wide control of the epidemic.

Software and code

Posterior distributions were sampled with Markov chain Monte Carlo (MCMC) simulation performed using MCSim v.6.1.0 in Metropolis within Gibbs sampling³⁶. For each US state, four chains of 200,000 iterations each were run, with the first 20% of runs discarded and 500 posterior samples saved for analysis. For each parameter, comparison of interchain and intrachain variability was assessed to determine convergence, with the potential scale reduction factor R ≤ 1.2 considered converged³⁷. Additional analysis of model outputs was performed in RStudio v.1.2.1335 (ref. ³⁸) with R v.3.6.1 (ref. ³⁹).

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.